Aufgabe 1:
Bilden Sie die Ableitung der Funktion f mit f(x)=(4+e3x)5.
(2 VP)
Aufgabe 2:Berechnen Sie das Integral
.
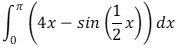(2 VP)
Aufgabe 3:Lösen Sie die Gleichung (x3-3x)(e2x-5)=0.
(3 VP)
Aufgabe 4:Der Graph einer ganzrationalen Funktionen f dritten Grades hat im Ursprung einen Hochpunkt und an der Stelle x=2 die Tangente mit der Gleichung y=4x-12.
Bestimmen Sie eine Funktionsgleichung von f.
(4 VP)
Aufgabe 5: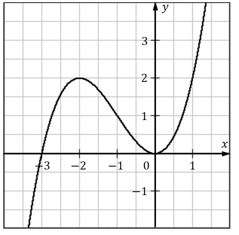
Die Abbildung zeigt den Graphen der Ableitungsfunktion f' einer ganzrationalen Funktion.
Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind.
Begründen Sie jeweils Ihre Antwort.
(1) Der Graph von f hat bei x=-3 einen Tiefpunkt.
(2) f(-2)<f(-1)
(3) f''(-2)+f'(-2)<1
(4) Der Grad der Funktion f ist mindestens 4.
(5 VP)
Aufgabe 6:Gegeben sind die drei Punkte A(4|0|4), B(0|4|4), C(6|6|2).
a) Zeigen Sie, dass das Dreieck ABC gleichschenklig ist.
b) Bestimmen Sie die Koordinaten eines Punktes, der das Dreieck ABC zu einem Parallelogramm ergänzt.
Veranschaulichen Sie durch eine Skizze, wie viele solcher Punkte es gibt.
(5 VP)
Aufgabe 7:Gegeben ist die Ebene E:4x1+3x3=12.
a) Stellen Sie E in einem Koordinatensystem dar.
b) Bestimmen Sie alle Punkte der x3-Achse, die von E den Abstand 3 haben.
(3 VP)
Aufgabe 8:Ein Glücksrad hat drei farbige Sektoren, die beim einmaligen Drehen mit folgenden Wahrscheinlichkeiten angezeigt werden:
Rot 20% Grün: 30% Blau 50%
Das Glücksrad wird n-mal gedreht.Die Zufallsvariable X gibt an, wie oft die Farbe rot angezeigt wird.
a) Begründen Sie, das X binomialverteilt ist.
Die Tabelle zeigt einen Ausschnitt der Wahrscheinlichkeitsverteilung von X:
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ... |
| P(X=k) | 0,01 | 0,06 | 0,14 | 0,21 | 0,22 | 0,17 | 0,11 | 0,05 | ... |
b) Bestimmen Sie die Wahrscheinlichkeit, dass mindestens dreimal rot angezeigt wird.
c) Entscheiden Sie, welcher der folgenden Werte von n der Tabelle zugrunde liegen kann: 20, 25 oder 30.
Begründen Sie Ihre Entscheidung.
(4 VP)
Aufgabe 9:Mit
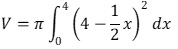wird der Rauminhalt eines Körpers berechnet.
Skizzieren Sie diesen Sachverhalt und beschreiben Sie den Körper.
(3 VP)